The Elusive Art of Shorting: Why It’s Hard to Win Big on the Downside
Exploring why puts are expensive, IV skews against shorts, and finding asymmetric payoffs remains a challenge.
The Intellectual Delight of Shorting
Most people dream of getting rich by picking that one stock—or a basket—that soars endlessly. My dream? A little more sadistic: getting rich by shorting that one overpriced stock.
I can't quite explain it, given that 99.9% of my wealth has been built by being long and optimistic about the market. But every now and then, I look at a stock and think—how cool would it be if I shorted this against market sentiment, against everyone around me… and was right? There’s an intellectual thrill in winning with a short.
When I kicked off my Special Situations portfolio, I planned for a 70/30 or 80/20 long-short split—a structure that lets me bet on both undervaluation and overvaluation while reducing correlation to the overall market. My screeners keep surfacing short opportunities, yet I’ve passed on all of them. This post is about why.
Shorting is Harder Than It Looks
Stocks follow Newton’s first law of motion: a stock in decline tends to keep declining, and an uptrend keeps running—until an external force intervenes. When dealing with overinflated or deeply fallen stocks, the chances of being right might be 50%, or likely even lower. To succeed as a special situations investor, there are two paths to an edge:
1️⃣ Be right only 25-30% of the time—but structure bets so that even with a low win rate, you come out ahead.
2️⃣ Find an informational edge that lets you be right far more often.
I’ve chosen the first path. My trades are structured for asymmetric payoffs: a 4x or 5x return on wins, knowing full well that losses will go straight to zero. Collectively, that should still be a win.
Finding 4x or 5x opportunities for long positions is easy—bull spreads and even outright call options can deliver those payoffs. But short trades? A nightmare.
Puts are expensive. At best, I can structure a 3x payoff, but often it’s closer to 2x. Shorting is already difficult—especially in this endless bull run—but doing it with low payoffs makes no sense.
The Curious Case of Put Pricing
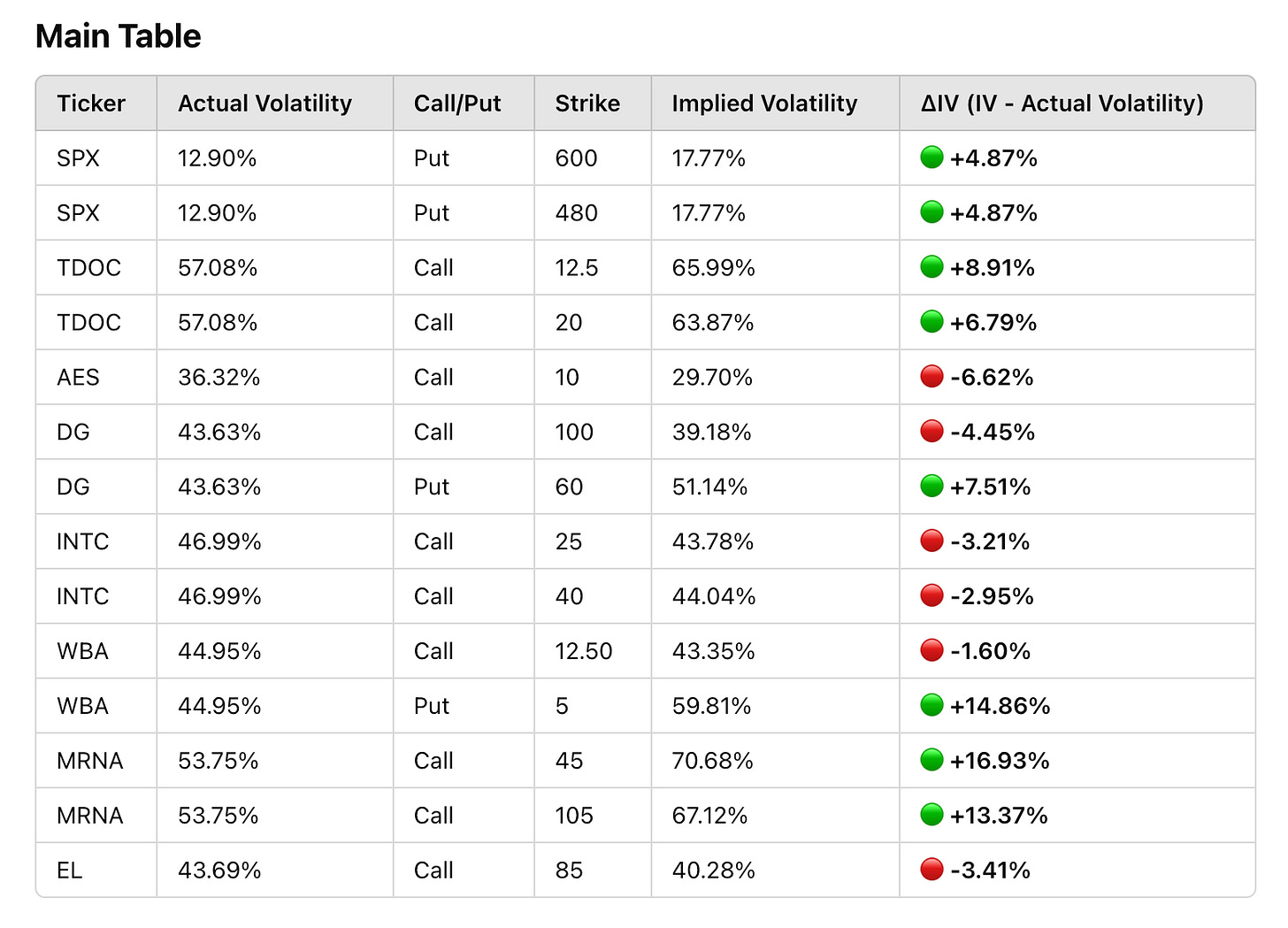
Why are puts so expensive relative to their expected returns? That’s what I set out to understand. The chart below compares implied volatility (IV) to actual volatility across several stocks over the past two years. The good news? Implied volatility generally tracks actual volatility, staying within 1.2x of realized volatility. Low-volatility stocks have cheap options, high-volatility stocks have expensive ones. So far, so good.
But here’s where it gets interesting:
In many cases, put options trade at significantly higher implied volatility than actual volatility, while call options don’t—sometimes, you can buy calls for IVs lower than actual volatility.
The IV Skew Puzzle
In options pricing, IV skew refers to the difference between put and call implied volatilities. A positive skew means calls are more expensive, while a negative skew means puts are pricier.
The pattern is everywhere, but it really stands out with Dollar General (DG) and Walgreens Boots Alliance (WBA). In both cases, put IV is higher than actual volatility, while call IV is lower, creating a massive negative IV skew.
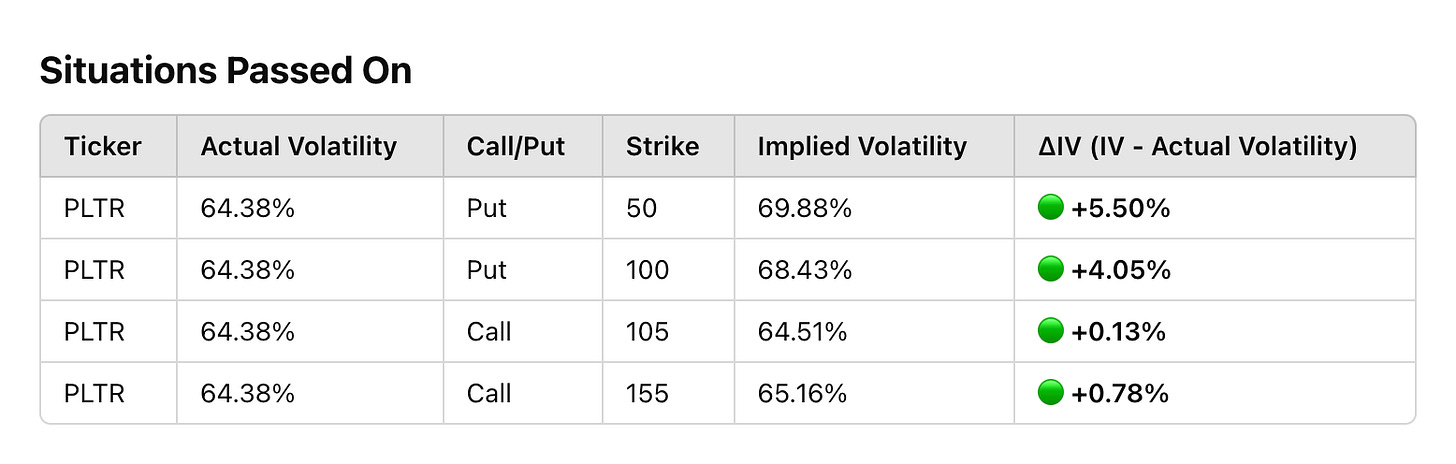
Another example: I briefly considered shorting Palantir (PLTR). Its put IV was ~5% above actual volatility, while call IV was less than 1% higher. That’s a -4% skew—meaning the market is pricing puts significantly richer than calls.
What Does It Mean?
I’ve never explicitly tracked this metric before, so maybe this is just how the market works. Or maybe this persistent negative skew signals something deeper—perhaps a sentiment-driven premium baked into puts.
Regardless, short trades with strong risk-reward payoffs remain elusive. The only thing that looks remotely reasonable? Shorting the market as a whole—where the trade-offs seem better than shorting individual stocks. But then, moving the market—especially downward—takes far more effort than moving a single stock. Newton’s second law in motion.
(ps: While all calculations are mutually consistent, they were made a while back, when drafting this post, but the post itself got delayed as I found more interesting content to get out. I strongly believe the delay doesn’t take anything away from the core message.)
Happy Investing!
Disclaimer: I am not your financial advisor and bear no fiduciary responsibility. This post is only for educational and entertainment purposes. Do your own due diligence before investing in any securities. I may hold or enter into, a position in any of the stocks mentioned above. The above is NOT a solicitation to either buy or sell the securities listed in this post.