Options: Understanding Pricing Parameters
Volatility & Distance from Strike Price is what matters
This post is a continuation of my previous post - Options: A Primer - it is best read with that context in mind.
History of Options Pricing
Till 1968, options were not priced by the market in any consistent manner. Market participants (investors, traders, institutions etc) largely bought and sold options on gut feel, very often creating “free money” situations. In 1968, Economists Fischer Black and Myron Scholes produced a breakthrough by prescribing a formula by which the options could be priced relative to various parameters affecting the security. The paper titled The Pricing of Options and Corporate Liabilities (pdf here), took 5 years to get published.
Soon after the eventual publication of the paper in 1973, Robert Merton followed soon after with his paper Theory of Rational Option Pricing and Black-Scholes Model (pdf here), which eventually brought together the mathematics and the trading side of it. Some 3 decades later, this work was considered worthy of a Nobel Prize, but due to Fisher Black’s death before the Nobel prize was awarded, and hence rendered ineligible, only Merton and Scholes got the Nobel Prize, in 1997.
The Nerdy Stuff part 1
The actual formula is scary and for the mathematically inclined, here it goes.
//Where
C = call option price/premium
N = CDF of the normal distribution
S_t = spot price of an asset
K = strike price
r = risk-free interest rate
t = time to maturity
𝝈 = volatility of the assetTo be honest I am yet to even getting close to understanding it at its equation level, but let me not prevent my lack of intellect or my laziness come in the way of deciphering the relationships between the parameters. For most of us, what matters is how these parameters play with each other.
The price of an option goes up with volatility, interest rates and time to maturity. The Strike Price and Spot Price play some interesting games with the price/premium of an option - we will get to it in a bit. For the moment, just remember that there are 3 independent parameters and the relationship between two others (Strike and Spot price) that eventually affect the price of an option.
The Nerdy Stuff part 2
Eventually the price/premium of an option has 2 components to it:
The time value - the value that the purchaser gets to hold the option for a period of time and enjoy the asymmetric nature of an option.
The intrinsic value - if the option’s strike price is below the spot price (for a call option), then if nothing changes, then the option is surely to be exercised and the difference between the values is assuredly embedded into the option now, and hence that gets valued according. Think of it this way - if you showed up at an insurance company site, told them that you need an insurance that needs to pay you for 10$ of claim incurred this morning, then the insurer would want to add that $10 into whatever else they think should be the premium. That $10 is the intrinsic value.
The intrinsic value can be expressed mathematically as max(0, Spot - Strike) for Call options and max(0, Strike - Spot) for Put options, or thus in a piece of code:
intrinsic_value = (call_type == 'C') ?
max(0, spot_price - strike) :
max(0, strike - spot);The formula itself doesn’t separate the two out, but this is what it ends up looking it.
Relationships with Parameters
Let’s now go through the relationships through a series of graphs.
Volatility vs Options Price/Premium
Price/Premium of an option is directly proportional to the volatility of the underlying asset. The relationship is linear.
(note: For the rest of the graphs, I have used 50% as a volatility which is an arbitrary choice and kept constant in order to show the relationship with other parameters. The actual volatility may be higher or lower for any given security at any given time, and changes with the duration of the option.)
Interest Rates vs Options Price/Premium
The price/premium of an option is also directly proportional to Risk Free Interest rates, and the relationship is linear but with a much lower slope.
In fact the slope is almost negligible compared to that of volatility. Volatility only needs to move from 50% to 60% (something that happens routinely many a given trading day in most securities) to move the options premium from $2 to $2.50, but with the same parameters, the interest rates have to move from 1% to 11% to achieve a movement from $2 to $2.20!
Days To Expiry (DTE) vs Options Premium (and Premium/day)
The premium of an option goes up with time, moving from 1% for a single day, to about 30% for a 2 year period (with volatility being constant at 50%). This is naturally to be expected. The holder of the premium in the first case has only one day to benefit from the movements of the security, while in the latter case has a good two rounds around the sun.
However, the premium per day of an option rapidly declines with the length of the premium. So, while a one day option is about 1% (and hence 1% per day), one with a 2 year expiry is a mere 0.04% per day.
Almost like buying any other commodity (say bananas), a wholesale lot of options is cheaper than a retail lot of options. Who says options pricing is complicated?
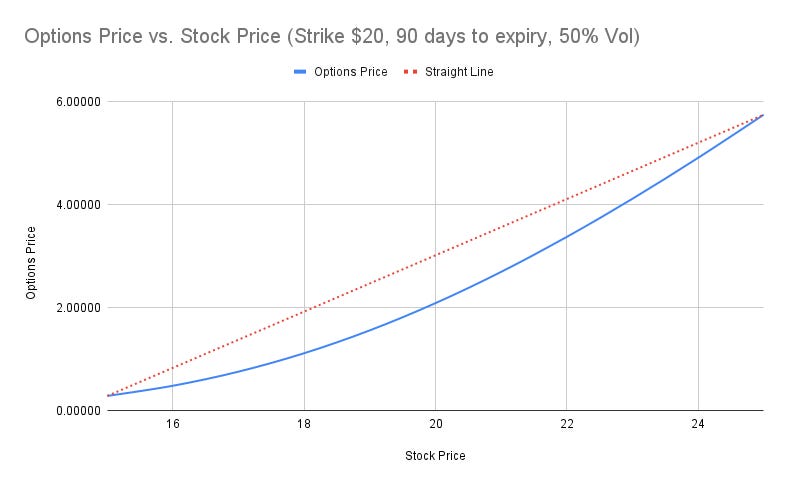
Stock price vs Options Price/Premium
Given the same strike price, the options price (aka premium) changes in concave upward manner when the price of the underlying goes up. It moves under the straight line path between any two prices of the security.
The volatility of the options premium is higher than that of the underlying and the relative volatility of the option is not a constant. It depends on the other parameters discussed above.
Concluding note
Remember that none of the parameters used in the formula is constant. The price of the security & volatility is jumping around each trading day. On the other hand, days to expiry (duration of the option) and the interest rates move relatively slowly and perhaps a bit more predictably.
Effectively the premium of an option is jumping around all the time, when any of the parameters listed above moved around. This is one of the reason it is so easy to be caught on the wrong side of an option.
What is Implied Volatility?
Very often you will hear the term “implied volatility” or imp-vol or even IV in short. The only attribute of an option directly visible to us (outside of Strike Price and days to expiry, DTE) is the price/premium. Embedded into this is a volatility measure, but it is not exposed directly. Since market participants (a/k/a traders) want to use volatility information to make decisions, what they do is reverse engineer the volatility implied by the price/premium of an option given all the parameters being constant. This is why it is called “implied volatility”.
On its own, an implied volatility number (like 50%) is useless, but traders compare it to what they think it should be, or what it has been in recent past. Hence you will hear phrases like “volatility jumped”, which basically means options price have gone up, keeping all other params roughly the same.
Summary
I didn’t plan to write a multi-part series on options, but it is turning out that way. It is bad news for you - you have to read through the many parts and likely wait while the pieces come about. On the other hand it is good for me, as I get to think through the topics and extend the treatise if needed. Sorry, you are stuck with me for a bit.
Remember again, that as long term investors, we don’t need to trade in options at all, but knowing the tools of the trade might come in handy once in a while.
Disclaimer: I am not your financial advisor and bear no fiduciary responsibility. This post is only for educational and entertainment purposes. Do your own due diligence before investing in any securities and/or options.